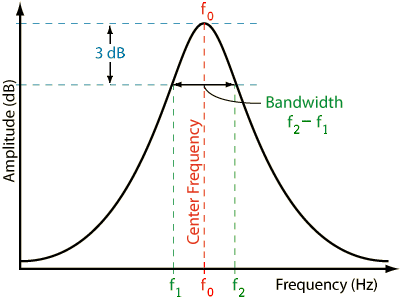
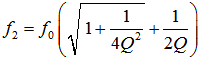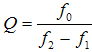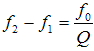합성이론 10: Modulation

처음 9개의 강의에서 정말 여러 가지 분야를 다루어왔지요.  waveforms, filters, envelopes, triggering, gating 등등. 이제 제법 합성에 대해 알아간다고 생각하실지 모릅니다. 아마 우리는 지금까지 waveform을 골라서 원하는 필터를 사용하여 수정하고 envelope옷을 입혀주어서 다이나믹을 만드는 정도는 쉽게 할 수 있게 되었다고 해도 되겠지요? 하지만 이것으로는 우리의 강력한 욕구가 만족되는 것은 아닙니다. VCF나 VCA등을 함께 사용한다고 해도.. 소리는 왠지 살아있지 않은 느낌이 들지도 모르지요. 소리가 삑삑 거리기만 하는 것은 아닌지..
지금까지 놓친 것 중에서 가장 큰 것이 바로 modulation이라는 놈입니다. 이것은 소리에 숨을 더해준다고 해도 과언이 아닙니다. 만약 여러분이 이것을 단순히 비브라토를 더하기 위해서 LFP정도를 사용하는 거라 생각한다면 큰 오산입니다.. Modulation은 의심의 여지없이 가장 깊고 난해한 부분입니다. 제가 처음 전자음악 이론을 공부할 때 Modulation 에 대한 이해가 쉽지 않았음을 아직도 정확하게 기억을 합니다. 또한, 많은 전자음학도(?)들 역시 여전히 Modulation 에 대해 잘 알지 못하고 있음을 알고 있습니다. 자.. 모르면 배우면 되는 것 아닐까요? 이제 단순한 접근으로부터 시작해 봅시다.

1. 단순한 3개의 Modulations

그림 1 은 우리가 이전에 공부한 1~9장까지의 시리즈에서 가장 중요한 요소들을 합쳐놓은 것입니다. 단순한 것에 연결되어있지만 신디사이저 형태에 유용한 형태입니다. 보다시피 신호소스가 tone generator(예:oscillator)로 들어갑니다. 출력은 처음에 Filter를 거치고 amplifier를 거쳐서 나가게 됩니다. contour generators는 소리에 ‘shape’를 입혀줍니다. 따라서 filter와 amplifier가 소리를 밝게 하고 크게 하는 등의 효과를 줍니다.

지금 어떤 사람이 바이올린이나 첼로를 연주한다고 가정해봅니다. 여러분이 알다시피 연주자가 악기의 어느 목 부분을 누르는 것에 따라 소리의 음높이가 결정이 되죠. 더 짧게 현의 길이가 주어질수록 음높이는 더 높아집니다. 지금 연주자가 연주한다고 상상해보고, 그 사람이 손목을 앞뒤로 흔드는 것을 상상해보세요. 크게 생각해보면, 그가 하는 것은 편의 길이를 살며시, 아주 적은 양이나마 길게-짧게-길게-짧게 해주는 것입니다. 맞지요? 그리고 여러분이 아시다시피 이것이 바로vibrato입니다.

그림 2 는 짧은 비브라토가 어떤 음의 음높이를 변하게 해주는 순간을 보여줍니다.

마찬가지로 그림3 은 vibrato의 한 주기 동안에 파형의 변화를 보여줍니다. (과장된 형태임)

이것을 analogue synth에서 만드는 것은 쉽습니다.  여러분은control voltage를 oscillator에 적용시켜서 음높이를 살짝 변형시킬 수 있습니다.

이 그림 4를 보시면 중간에 CV(the modulating waveform)dl LFO에 적용된 것을 볼수있습니다. 또한 그림을 잘 보면 VCA 가 modulating waveform의 amplitude에 관여한다는 것을 알수 있구요. 그리고 VCA 그 자체는modulation wheel로 조절됩니다. VCA 와 wheel 은 여기에서 아주 중요한 요소가 됩니다. 왜냐하면, 그것들 없이 vibrato의 양을 조절하는 것은 아주 복잡한 일이 되어버리지 때문입니다. 그리고 그렇게되면 음악적인 소리를 만드는것도 힘들게 되겠지요.

-Tremolo
vibrato에서 tremolo로 옮겨봅니다.  두 단어를 놓고 보니 여러분들 중에서 아.. 핵갈려. 하시는 분들이 있지요? 그럼 제가 명백하게 구분해드릴게요.

-음정이 변화한다:  Vibrato
-소리의 크기가 변화한다: Tremolo

입니다. 즉, 아까처럼 현악기 주자가 현을 길게 짧게 하는 것을 vibrato로 기억하시면 쉽겠죠? 그럼 Tremolo를 똑같이 현악기로 기억하려면, 연주자가 아까와 반대로 오른팔, 활대를 쥔손을 이용해서 힘을 주었다가 뺐다가 하는 것을 상상해봅니다. 아주 빠른 트레몰로를 만들긴 쉽지 않겠지만, 이론적으로 적용되고 기억하기 쉬운 예가 되겠습니다.

그림6은 그림3과 같은 양상이지만 그림은 아주 다른 모습을 보여줍니다. Frequency는 지속되지만 그 level은 시간에 따라 변화를 것을 확인하세요.

지금 우리는 두 가지 방식의 차이를 이해하고 있습니다. 둘간의 synthesizer 차이를 아는 것은 쉽습니다. 하지만 vibrato는 어떤 것이 oscillator의 ‘pitch’를 변화시켜 주어야 합니다. 하지만, tremolo는 signal chain의 끝에서 오디오 amplifier의 ‘gain’을 변화시켜 줄 것이 필요합니다. 다음 그림 7에서 확인해보세요.

세 번째로 소개할 그 녀석은 우리가 단순한 신디사이저의 voltage-controlled filter 을 변형시킬 때 발생합니다. 그 결과는 아마도.. 조금 더 어렵게 느껴질 것입니다. 실제로 여러분은 3개의 다른 modulation을 단순히 LFP의 frequency를 변화시켜주어서 만들어 낼 수 있습니다. 가장 느린 진동을 만들어서 (약 0.1Hz정도?) 여러분은 아주 느린 filter sweep을 만들어서 쉽게 확인해 볼수 있습니다. 그 속도를 1 ~ 2Hz 로 증가시키면 이 소리는 점점 wah-wah effect처럼 들리게 됩니다.(그림10) 만약 여러분이 계속적으로 소리를 증가시키면 (10~20Hz), 여러분은 아마도 으르렁거리는 소리를 듣게 됩니다. 그리고 이런 효과는 금관악기소리를 만드는데 유용하게 쓰입니다.

이런 modulation는 그리기도 쉽지 않습니다.(그림9)

왜냐하면 모듈레이트된 filtering때문에 일어난waveform에있는 변화가 아주 미세하기 때문입니다. 하지만 여러분이 아주 쉽게 소리의 차이를 귀로 확인할 수 있습니다. 그러나, cutoff frequency 가 낮을 때, 그리고 amplitude 가 아주 작게 떨어질때에는, 그 변화를 보기위해서 oscilloscope가 필요합니다.

물론 왜 이런 모듈레이션들이 서로 다르고 이것이 LFO와 연관되어있는지 특정한 이유가 없습니다. 더 나은 synth는 개별적인 LFOs를 사용하여 여러분이 각각의 소리에 적용할 수 있게 하며 각각 효과의 depth를 조절할수 있게 해 줍니다. 이것을 하기 위해서 장비들은 modulation wheels, aftertouch (pressure sensitivity), foot pedals등을 가지고 있는것입니다.

그림 11은 위에서 말했듯이 신디사이저가 여러 개의 modulation controller를 사용하는 것을 보여줍니다. 좀 겁나죠? 하지만 잘 보면 그다지 여려운 그림은 아닙니다.
그러나 이것이 세개의 modulation VCA들의 level을 control하는 것이 아닙니다. 따라서 여러분은 부수적으로 VCA들에 controller들을 연결시키는 것을 생각해야 합니다.

2. 또다른 단순한 Modulation
또다른 것이 기다립니다. 이것은 가장 좋은 아날로그 신디사이저와 대체될수 있습니다. 이것을 이해하기 위해서 low-pass filters 에 대해서 이야기했던 부분을 다시 한번 생각해봅니다. (합성이론 4장)
그림 12는 square wave(pulse waveform)입니다.  분명 square wave는 waveform에서 특이한 놈입니다. 이것은 신호가 꼭대기, 바닥 에서만 존재합니다. 따라서 이런 형태를 보이지요. 그리고 그 ratio는 천장, 바닥에서 얼마나 오래 머무르느냐에 따라 결정되는것이지요. 우리는 이 ratio를 ‘duty cycle’이라 합니다. square wave 가 정확하게 꼭대기에서 할당시간의 반을 차지하기 때문에 비율(ratio)은 1:2가 됩니다. 그리고 우리는 duty cycle이 50%라고 합니다. 만약 1:3이 되면 33.3%가 되겠죠. 그리고 꼭대기에서 1/3의 시간을 할애하겠습니다. (그림13)

그리고 1/4은 25%가 되고…..(그림 14)

(참고:50%보다 더 큰 duty cycle에 대한 언급을 볼수 있는데, 필수적으로 어떤 수 X가 0~50에 높였을 때에 duty cycle  (50+X) percent 는 (50-X) percent와 같게 되지만 ‘ phase ‘는 반대로 됩니다.)

서로 다른 duty cycle을 가진 Pulse waves은 아주 다른 소리를 만들어 냅니다. 좁은 cycles (5~10%)은 아주 가늘고 비음과 같은 소리를 냅니다.(오보에 상상) duty cycle이 50%에 가까워지면 소리가 두꺼워 진다고 생각할수 있습니다. 정확히 50%가 되면 텅빈소리와 같은 것을 만들어냅니다. 네..슬슬 감이오죠? 언제나 예로 나오는 바로 그 클라리넷소리!

이런 음색변화는 어디서 온다구요? 네.. 바로 어떤 하모닉스가 존재하느냐 에 따라 다르다는 것 제가 저.. 앞에서 이야기 한적이 있습니다. 그리고 그 각각의 partial이 지닌 amplitude의 영향도 있겠습니다.
pulse wave 는 sawtooth 와 같은harmonic 분배를 가집니다. 하지만 한가지 다른점은 duty cycle of 1:n (n:정수) 모든 n번째harmonic은 spectrum에서 빠져있다는 것입니다.!! (이해가 안가시면 합성이론 1장 참고)

다시 square wave를 봅니다. 이것은 duty cycle 이 1:2이기 때문이 우리는 모든 두번째 배음이 빠져있다는 것을 생각할 수 있습니다. Pulse wave관계에 대해서 정의한 우리의 법칙은 여기저기에서 많이 등장하지만 종종 이해되지 않은채 알고있는 경우를 보게됩니다. : 모든 짝수 하모닉이 빠져서 square wave는 1st, 3rd, 5th, 7th,.. 의 홀수 하모닉으로 구성되어있는 것입니다.

다시 위의 그림 13 , 14를 봅니다. 이것은 duty cycles 1:3, 1:4를 가집니다. 결과적으로 33.3% pulse wave가1st, 2nd, 4th, 5th, 7th, 8th…harmonics 를 포함하고 있습니다.(모든 3번째 harmonic 빠짐), 그리고 25 percent pulse wave 는 1st, 2nd, 3rd, 5th, 6th, 7th, 9th, 10th…….. harmonics .(모든 4번째 harmonic 빠짐)
그럼 만약에 이 숫자가 정수가 아니면 어떤 결과가 나올지도 궁금해집니다. 예를들어 만약 28.5%의 pulse wave면? 28.5 percent 은 1:3과 1:4의 중간 어디엔가 존재하지요? 모든 3번째 하모닉이 다소 감소하고, 4번째도 그렇습니다. 그러나 signal로부터 하모닉스가 아주 없어지지는 않습니다.

이제 어느정도 감을 잡고계신가요? 이제 좀 끝나가나 싶지만 이제 시장입니다. 이제 우리는 ‘Pulse Width Modulation’을 만들기 위해서 pulse widths 와 modulation의 지식을 결합해 볼 것입니다………
이것은 두번째 CV input을 oscillator로 연결합니다. (frequency를 modulate하는 대신) 이것은 duty cycle을 변화시킬수 있게 해 줍니다.!! (cool~). 만약 LFO 가 modulating CV를 제공하면, 결과가되는 waveform은 그림 15와 같을 것입니다.

이것은 그림 16에 의해서 만들어집니다.

이 그림 16은 일반적으로 풍성한 합창 같은 소리를 만드는데 사용됩니다. 비록 Pulse Width Modulation이 주로 pulse waves에 적용되지만 또한 여러분은sawtooth waves에도 적용할 수 있습니다. 물론 여러분이 이것을 위와 똑같이 duty cycles로 적용시키는 것은 아닙니다. 이것은 또다른 범위의 섬세하게 다른 음색을 만들어 줍니다.
Pulse Width Modulation은 string ensemble sounds를 만들거나, 풍성한lead synth patch에 유용합니다. 하지만 이것을 다른 chorus effect와 혼동하면 안됩니다. 들어오는 소스에 각각의 harmonics의 amplitude를 modulating하는것과 독창적인 소리를 만들어 내는 부분 등에서 이것은 다소 차이가 있습니다.

3. 들을 수 없는 저 음속에서부터 Audio Frequencies까지
모든 형태의modulation은 하나의 공통점을 가집니다. : low-frequency oscillators를 modulating control voltages로 사용한다는점.
그러나 만약 우리가 oscillator, filter, amplifier (또는 pulse width까지)를 audio-frequency (AF) signals 을 이용하여 modulate하면 어떨까요? 우선 우리는 아마 아주 빠른 vibrato, tremolo, growl(으르릉소리), 또는 Pulse Width Modulation,을 들을 수 있다고 생각할수 있습니다. 그러나 그렇지 않습니다. audio frequencies를 modulate하는 것은 완전 완전 다른 이야기입니다. 그러나 이것은 다음 시 간 에 계 속 됩 니 다!!!

합성이론 12: Frequency Modulation

얼마나 많은 사람이 소리 합성의 새로운 형태를 발견할 수 있을까요? John Chowning은 1960년대 중반에 Stanford University에서 vibrato의 새로운 형태를 실험하던 중, 우연히 새로운 것을 발견했습니다. Signal을 modulate하는 frequency가 어떤 점 이상으로 증가하게 되면, vibrato는 modulate된 음으로부터 사라져 버린 후에 복잡하고 새로운 것으로 대체되어 버린다는 것입니다. 그가 가장 공통의 encoding technique 인 공중파 라디오 FM이 무엇인지를 밝혀냈다는 것을 알수 있습니다. 그러나 그의 발견이 가졌던 특별한 점은, 아주 높은 frequency(들을 수 없을 정도로)를 다루고 있는 라디오 기술자와는 달리, Chowning가 modulate된 wave를 들을 수 있었다는 것입니다.  그는 FM이 가장 강력한 합성방법이라는 것을 1966년에 발견했으며, 그것을 이용해 가장 먼저 음악을 만들고 녹음한 장본인이 되었습니다.

Chowning과 그의 동료는 그 후 몇 년을 FM을 연구하는데 정성을 기울였고, 그들이 성취해 낼 결과를 위해 소리의 수학적, 실용적인 방식에 초점을 맞추었습니다. Chowning 은 그때 Stanford University Licensing Office에서 이런 합성이 많은 미국의 제조업자들이 이것을 상업적 목적으로 사용할지 가늠하기 위하여 그들에게 접근하였습니다. 당시에 Minimoog 와ARP Odyssey 가 지배적이었을 때, polysynths 는 electronic engineer들의 눈에 봤을 때 아주 번뜩이는 놈이었지요. 그리고 또한 4-bit microprocessors 는 완전 예술의 경지였습니다. 그러나 그 어떤American manufacturers도 FM의 잠재적인 능력을 알아보지 못했습니다. 따라서 이것은 거의 절망적인 상태가 되어서Stanford에서Yamaha로 넘어갔습니다. Ichimura라는 엔지니어가 제때에Chowning를 알아보았고, 그들은 이것이 역사가 될 것이라는 것을 알아보게 되었습니다.

80년대 전반에 걸쳐 야마하는 어마어마한 숫자의FM synthesizers, 오르간, 키보드를 파는 데에 성공했고, 우리는 지금 FM을 하나의 실용적인 디지털 처리로 생각하고 있습니다. 그러나 지금 하려는 것은 그것이 아닙니다. 그것은 조금 더 실용적이고 디지털 형식아래에 실용적으로 사용될 수 있지만, FM의 이론은 단지 아날로그 오실레이터에 적용할 수 있는 것과 같은 것입니다. 그럼 한번 볼까요?

1. 한번 더, 수학의 세계로~
지지난번에 Amplitude Modulation에서 몇몇 새로운 소리를 만드는 방법에 대해서 설명했습니다. 조금 기억을 되살려볼까요?. 공식 1과 2는 2개의 가장 단순한 파형인 sinewave를 보여줍니다. 그 순간의 amplitudes 는(어떤 시간에 주어진 level-, ‘A’)는 그것의 gain과 관계가 있습니다. (최대amplitude가 cycles에 도달할 때 ‘a’), 그밖에 frequencies (‘w’) time (‘t’).그리고, 이전처럼 ‘1’ 는 ‘2’  waveform 1 과 2 입니다.

이전을 생각해보면 여러분은 또한 우리가 첫번째 wave의 최대 amp값을 VCA의 gain으로 정의내렸던 것을 기억하실 것입니다. (안나시면 다시 예전파트를 사사삭), 그리고 우리는 두번째 wave로 modulate를 했었지요. (그림1)

공식3은 어떻게 적용시켰는지 보여줍니다.

그러나 지금부터 우리는 무엇을 조금 더 섞어보려 합니다. 첫번째 wave의 modulating대신, 우리는 frequency를 modulate해야겠지요? 그림 2에서 보이는block diagram 에서 단순하게 보여준 것 처럼해 볼것입니다. 공식4에서 FM을 보여줍니다. 이것은 AM때보다 조금 으시시 해 보입니다. 사실살 여러분이 조금 더 자세하게 봄다면, 지난번과 같은 양상을 가지고있다는 것을 아실 수 있을 것입니다. 단지 frequency에 A2만 들어가 있습니다.

만약 우리가 지난번에 한 공식4, 5번을 되살려본다면, 같은 방식으로 여기에 적용할때에 어렵지 않을 것입니다. 그럼.공식5는 다음과 같이.

여기서 여러분은 완전히 그 고지를 향해 뛰고 달리고 땀을 흘리고 계실 겁니다. 지난번 공식과는 다르게(우리가 다루었던 공식의 수준을 생각해 보면) 이번 것은 거의 괴물입니다. 참으로 여러분은 조금 더 과중함을 느낄 것입니다. 그러나 일단 풀리는 공식까지 끌고 가봅시다.

2. FM 은 단순히 아주 빠른 Vibrato…
이번에는 합성이론10장으로 돌아가봅니다. 그림 3을 보세요

그림3 은 어떤 waveform( ‘Carrier’) 에서 그것의 frequency가 modulation에 의해서 위아래로 왔다 갔다 하는 것을 보여줍니다. 이번 예에서 그Modulator의 frequency는 Carrier보다 낮다는 것에 초점을 맞춰봅시다.

지금 그럼 Modulator의 frequency가 증가하여 Carrier에 거의 같은 순간까지 접근하여, 같아지고, 그 다음 그 레벨을 넘어선다면.?  여기서 Carrier wave에 주기적으로 ‘압축’되고 다시 ‘펴지는’것처럼 보이는 대신, modulation은 Carrier wave의 각 주기 이내에서 distortion형태가 될 것입니다. 이것을 설명하기 위해서 아주 짧은 Carrier를 예로 들어보겠습니다. 그림4는 한 주기의 1/8정도입니다.

이제 여기에 Modulator를 적용시켜 봅니다. 이 예의 amplitude는 낮게 설정됩니다. 그러나 Carrier의 frequency는 몇배가 됩니다. (그림5)

(그림5는 7주기보다 많은modulation이며 carrier주기의 1/8을 보여줍니다. 즉 Modulator frequency는 대략 Carrier의 60배가 됩니다.) 이것을 이해하였다면 그 소리는 vibrato와 거리가 멉니다. 그럼 무슨 소리같이 들릴까요? ) (그림5)

3. Side Bands, Side Bands, …
다시 공식5를 봅니다. 여러분은 A1 이 다른곳에서부터 2개의 용어를 데리고 온 것을 볼 수 있습니다.t: a2 와 w2. 이것은 물론 gain (maximum amplitude)과 Modulation frequency입니다. 따라서 이것들 각각은 modulate되는 신호의 속성에 영향을 끼칠것을 예상할 수 있지요. w2를 먼저 보면서 그 출력에 영향을 끼지는 것이 무엇인지 봅니다.

John Chowning은 FM이 AM처럼출력 신호의 frequency spectrum에서 side bands를 만든다는 것을 발견했습니다. –부가적인 요소로서, 그러나 Carrier와 Modulator의 frequency와 관련된 화성적 관점이 아닌—어떻게frequency modulation이 side band를 만드는지 보기 위해서 frequency wc 를 사진sine wave Carrier 와 frequency wm 을 가진sine wave Modulator 를 봅니다. (그림6)

그러나 AM이 2개의 side bands (wc+wm) 와 (wc-wm)를 생성해 내지만, FM 은 조금 다릅니다. 아래의 공식6을 봅니다.

각 side band는 Carrier frequency plus minus  Modulator frequency의 정수 배와 같다. 라는 공식입니다. 물론 n은 어떤 정수가 올 수 있기 때문에 frequency modulation을 어떤 signal에 적용시키는 것은 무한대의 sideband series를 생성해 냅니다. (이론적으로). 하지만 실제로는 어떤 system도 무한대의 bandwidth를 가지지 않으며, analogue systems은 한정된 bandwidth이내에서side bands 를 만들어 냅니다. 이와 유사하게 digital FM systems의 제조업자들은 그들이 중요하게 여기는 이 값들의 계산을 강요적으로 시킵니다.

이런 가능한 요건에서 공식6의 단순함이 sedeband의 위치를 쉽게 보도록 해 줍니다. 그림 6에서 주어진 Carrier와 Modulator가 그림 7에서 side bands를 포함한 것을 볼 수 있습니다.

그럼 이것들의amplitudes는 어떻게 될까요? 자. 우리는 지금 frequency modulation이side bands를 만들어 내는 것을 보았고 그 Modulator’s frequency 가 그것들이 놓일 곳을 정해준다는 것도 알았습니다. 그러나 이것의 spectrum의 모양은 어떻게 생겼을까요?  이것을 대답하기 위해서 우리는 다시Modulator의 두 번째 성질을 생각해 보아야 합니다. – 그것의 gain, a2 – 그리고 새로운 개념인 ‘Modulation Index’를 소개할 차례입니다. 이것을 줄여’ß’ (‘beta’)라고 부르겠습니다.

ß를 설명하기 위해서, 다시 단순한 vibrato의 예를 생각해 봅니다. 단순한synthesizer patch를 상상하면서modulation의 amplitude가, Control Voltage source 에 의해 조정되는VCA 에 의해 변하는 것을 생각해보세요. (그림 8) 이 경우에 Modulator frequency wm 이 Carrier frequency wc.보다 아주 낮다는 것을 기억하면서.

VCA 의 gain이 zero이 되는 것을 생각해 봅니다. 분명 modulation은 없습니다. 그리고Carrier는 단순하고 변화하지 않은 톤을 생성해 냅니다. 지금 VCA의 gain을 조금 높여봅니다. 기대한 것처럼 아주 부드러운 vibrato를 만들어 냅니다. 그러나 그것을 멈추지 말고 계속 증가시켜서 Modulator가 Carrier를 넓은 범위의 frequencies영역을 오르내리게 해 봅니다. 이 시점에서 공습경보 시 울리는 사이렌과 같은 소리를 내게 됩니다. 이것을 통해서 우리가 알아야 하는 것은 우리가 듣는 그 소리가 단지 Modulator의frequency에 의해서만 결정되는 것이 아닌 gain또는 maximum amplitude의 영향을 받는다는 사실입니다.

이 아이디어를audio-frequency FM에 적용시켜봅니다. 우리는 반드시 우선 ß를 Carrier의 frequency sweep(오르내림)의 비율로 지정해야 합니다.(Carrier가 modulate되지 않은 frequency로부터 벗어나는 양)그것은 다음과 같습니다.

ß = the Modulation Index,
wc = Carrier frequency
wm = Modulator frequency.

이 식의 분자가 Carrier frequency에서 변화 량이기 때문에 ß 는 직접적으로 Modulator의 amplitude와 관련이 있습니다. 지금 이것의 조금 이상하게 여겨지는데 이것은 어떤 주어진 Modulator frequency에서Modulation Index(즉Modulator의 amplitude)는 출력 신호 spectrum의 각 성분의 amplitude를 결정하기 때문입니다.  (and, therefore, the amplitude of the Modulator)이해하고 따라가기 힘들다는 것 잘 알아요. 따라서 예제가 필요하겠지요?

자 그럼Modulation Index 가 낮은 경우를 보겠습니다. 0.1이하의 영역을 보겠습니다. 단지 주요한side bands가 Carrier에 근접하게 있을 것이며, 그 결과는 우리가 지난번에 AM하면서 보았던 것과 비슷할 것입니다. (그림9)  그럼 이번에 ß가 조금 높다 해봅시다. 한 5정도로 잡아볼게요. 그럼 우리는 이번에 더 넓은 시리즈의 side bands를 볼 수 있으며 더 많고 복잡한spectrum 의 결과를 볼 수 있습니다. (그림10)

처음 6개의 side bands는 ß=5에 의해 만들어 졌지만 실제 signal에 더 많은 것이 있습니다. 게다가 여러분은 이 ß값의 흥미로운 결과를 꼭 기억해야 합니다. 그것은: 원래 Carrier의 amplitude가 줄어들었다는 것입니다. 참으로 ß의 값은 결국 모두 사라지게 하는 결과를 주게 될 수 있습니다.!

다시 공식 7을 보겠습니다. 여러분은 분모가 Modulator의 frequency인 것을 보세요. 이것의 결과는 아주 중요합니다. 이렇게 말해볼까요? 여러분은 여러분의 원하는 음이 그림 10의 spectrum이 되도록 결정했다고 해 봅니다. 그리고 여러분이 그것을 키보드에서 위아래로 소리를 연주할 수 있게 되기를 원한다고 해보지요. 이것은 즉, Carrier와 Modulator가 키보드를 동등하게 track하게 되어야 합니다. 그리하여 spectral 요소(sidebands)사이의 화성적 관계가 계속 남아있어야 합니다. 그러나 공식7은 이렇게 설명합니다. : Modulator frequency 가 증가하면 ß 는 감소한다. 라고 말이지요. 예를 들어 만약 여러분이 한 옥타브 높은 소리를 연주한다고 하면 wm 는 2배가 되고 ß는 따라서 반이 되겠지요? 이런 spectrum의 변화를 피하기 위해서Modulator amplitude는 반드시 비례적으로 증가시켜서 ß 를 계속 지속하도록 해주어야 합니다. 그림 11에서 이것을 어떻게 해야 하는지 보여줍니다. 이런 배치를 조절하는 것은 어렵지 않습니다.  그리고 아날로그 성분의 변화가 아주 잘한다 해도 모순이 일어나게 됩니다. 따라서 FM은 거의 모든 상황에서 digital technology로 대체되어 사용되는 것이 좋겠습니다.

4. FM vs Analogue Filters
자 이제 우리는 bandwidth에 대해서 이야기해야 합니다. 처음에 공식 6의 이야기를 하면서 이야기했던 것이 있는데, 원래 소리 체계에서는 무한의 bandwidth의 신호를 처리할 수 없다는 것. 기억하시죠? 그럼 어떻게 처리되는지 살펴봅시다.
여러분은bandwidth를 주어진 신호에 의해 주어지는 frequencies의 범위로 정의해야 할 것입니다. 예를 들어 sine wave 가 100Hz라고 했을 때 이것은 대수롭지 않은 양의bandwidth를 가지고(어떤 특정 frequency에만 존재하는)있는 반면, 같은 기본음을 가진 waveform이 200hz에서 하나의harmonic을 더하고 있다면 이것은 100hz의 bandwidth를 가지겠죠? 마찬가지로, 신호가 100Hz ~ 1500Hz에 있다면 1400Hz의 bandwidth를 가지게 되겠구요. 이것을 FM 에서의 출력에 도입시켜 봅시다.

Carrier가 500Hz의 frequency를 가진sine wave라고 가정하고 Modulator 는 300Hz라고 해봅니다. 분명 여러분은 이것을 단순한 audio mixer를 이용해 mix할 것이고 위의 정의를 사용하면, 그 결과 200Hz 의 bandwidth를 가지는 신호를 볼 수 있게 되겠지요.

자 그럼 지금 그 시그널을 배열하여 Amplitude Modulation을 만들어 볼까요? 지난달처럼 우리는 3개의 결과 wc, wc+wm, wc-wm를 볼수 있겠네요. frequencies 는 500Hz, 200Hz, 800Hz 이구요. 따라서 결과로 나오는 신호의bandwidth 는 가장 낮은, 그리고 높은 sideband를 펼쳤다고 하면 600Hz(800-200)이 되겠네요.

자 그럼 지금 FM의 신호의 bandwidth를 생각해봅니다. 비록 이론적으로 무한대라 하여도(기억하시죠 side bands의series는 무한함) Modulation Index는 더 높은 ‘n’의 side bands가 하찮은 양의 amplitude를 가지고 있다는 것을 입증시켜 줄 것입니다. 즉. 이말인 즉! bandwidth 는? 유한하다!. 게다가 출력 신호의 bandwidth 공식이 요기에 있습니다.

B = bandwidth
wm = modulator frequency
ß = Modulation Index.
ß 가 아주 작다고 가정해 봅시다. 그때 위의 500Hz Carrier, 300Hz Modulator의 예에서 출력의bandwidth 는 2 x 300Hz x (1 + 0) = 600Hz. 따라서 작은 ß값은 AM을 사용하여 얻어진 것과 같아 보입니다.

그러나 ß=5라고 해봅니다. 그때 위의 예에서 bandwidth는 2 x 300Hz x (1 + 5) = 3,600Hz가 됩니다. 분명 큰ß 값은FM이 다른 어떤 방법보다도, 더 복잡한 신호를, 더 높은 bandwidth와 함께 생성해 낼 수 있도록 해줍니다. (그림12) 그리고 이에 관해서는 다음시간에 또 계속 할 것입니다.

차감합성(subtractive synthesis)에서, 소리의 볼륨의 변화는 종종 amplifier에서 나오는 contour gen에 의해 결정 됩니다. 유사하게, 소리의 tome에서 어떤 변화는 보통 필터의 cutoff frequency에서 나오는 contour gen에 의해 보통 결정됩니다.

FM 에서, 소리의 volume 은 여전히 volume envelope에 의해 결정됩니다. (물론modulate된 Carrier), 그러나 여러분은 더 이상 filter로 소리를 변형시킬 필요가 없게 됩니다. 왜냐. Modulator frequency 때문에, Modulator amplitude는 출력의 bandwidth 를 결정합니다. 여러분은 그림 13에서처럼 7개의 synthesizer modules를 사용하여 흥미로운 결과를 만들수 있습니다.

보다시피 EG2가 VCA2의 gain을 줄이는 것처럼 출력신호의amplitude 는 줄어듭니다. 따라서output 는 점점 더 조용해지고 조용해집니다. 동시에, VCO1에서 나온 Modulator의 최대amplitude 는 EG1이 VCA1의 gain을 증가시키는 것 처럼 증가합니다. 즉, 시간이 지나가면서 Modulation Index는 증가하고. Bandwidth도 증가하고, 출력은 점점 밝아지고 밝아집니다. 이것은 자연스러운 소리와 반대되는 점입니다. 소리크기가 증가한다는 것은 언제나 소리의 밝기와 상관이 있기도 합니다.

여러분은 아마 필터를 이용한 이런 영향(소리의 밝기)을 계속 반복하는 것 이외에 방법이 없다 생각할지도 모르겠습니다. 그리고 여러분이 contour generator 나 low-pass VCF 로 어떤 신호를 시간에 흐름에 따라 더 밝게 해줄수 있는 것 또한 사실입니다. 그러나 그 구성으로 FM된 소리에서 발생하는 복잡한 tonal 변화를 만드는 것은 불가능하지요? 따라서 방법의 선택. 여러분의 자유입니다

5. 요약하자면
공식은 다 잊고 요약해봅시다.

*주요한 spectral 요소의 양과 그것의 amplitudes는 Modulation Index에 의해 결정됩니다. 이것은 Modulator의 amplitude에 비례합니다. 그러나 반대로 Modulator의 frequency에 반비례합니다.

*어떤 주어진 Carrier frequency에서, spectral 성분의 위치는 Modulator의 frequency에 의해서만 결정됩니다.

비록, 이것을 입증하는 것(설명하기도 정말 힘들었습니다.)과 공식(이것두요 -.-) 은 정말 악몽 같지만, 그 근본은 쉽게 이해될 수 있습니다. 그리고 여러분이 FM을 아날로그, 디지털, 무엇을 사용하여 만들던지 이런 원리는 똑같이 남아있다는 것. 잊지 마세요.
그리고 오늘의 진짜 요점정리는?

Frequency Modulation 은 합성의 강력한 방법으로서 디지털의 합성으로서 아날로그 신디사이저, 그리고 디지털 신디사이저에 적절합니다. 그리고 어떤 다른 방법으로는 얻어질 수 없는 소리를 생성할 수 있게 됩니다.